• [D] Dong5k

  • 时间限制: 2000 ms　内存限制: 262144 K
  • 问题描述

  • It is well known that Dong5k have so much money. Dong5k plan to have a journey from (0,0) to (n,0). He need to design a tourist route.

    For each step, it is allowed to move only to go ahead (uphill, downhill or go straight) that means if Dong5k at point (x, y) in ith setp, he can go to one of the following point (x + 1, y + 1), (x + 1, y - 1), (x + 1, y) in (i + 1)-th step.

    Dong5k is so famous not only his wealth but his weight. Uphill and downhill demands great physical strength. So he can't choose more than one uphill or downhill in the continuous k steps, that means if he uphill (or downhill) in ith step, next time he uphill (or downhill) at least in (i + k)-th step.

    Calculate the number of different ways Dong5k can design.


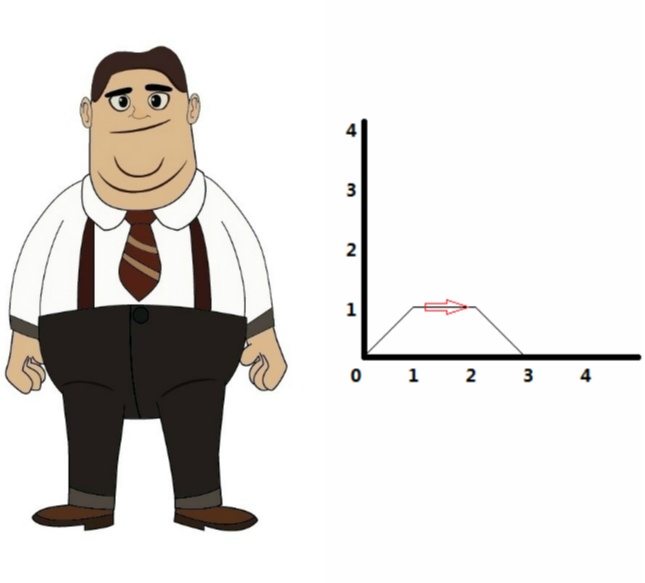
    Note: Dong5k can't under the ground, that means the y-coordinate must be equal or greater than 0 in each step.

  • 输入
  • First line, the number of test case T. (T <= 2000)
    For each test case, input will be two integers n , k(1 <= n, k <= 100000).
    In all test case, sum of n is less than 3000000.
  • 输出
  • Output the result modulo 1000000007(1e9 + 7).
  • 样例输入
  • 2
3 1
3 2
  • 样例输出
  • 4
2
  • 提示
  • In the first sample, there are four ways from (0, 0) to (3, 0):
1. (0, 0) -> (1, 0) -> (2, 0) -> (3, 0) 
2. (0, 0) -> (1, 0) -> (2, 1) -> (3, 0)
3. (0, 0) -> (1, 1) -> (2, 0) -> (3, 0)
4. (0, 0) -> (1, 1) -> (2, 1) -> (3, 0)
In the second sample, there are two ways from (0, 0) to (3, 0):
1. (0, 0) -> (1, 0) -> (2, 0) -> (3, 0) 
2. (0, 0) -> (1, 1) -> (2, 1) -> (3, 0)
  • 来源
  • cxlove @AHU
  • 操作

显示春菜