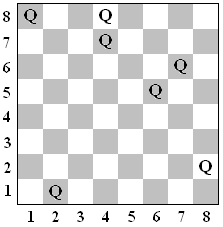
Figure 1	Figure 2	Figure 3

Lots of time has been spent by computer science students dealing with queens on a chess board. Two queens on a chessboard collide if they lie on the same row, column or diagonal, and there is no piece between them. Various sized square boards and numbers of queens are considered. For example, Figure 1, with a 7 x 7 board, contains 7 queens with no collisions. In Figure 2 there is a 5 x 5 board with 5 queens and 4 collisions. In Figure 3, a traditional 8 x 8 board, there are 7 queens and 5 collisions.

On an n x n board, queen positions are given in Cartesian coordinates (x, y) where x is a column number, 1 to n, and y is a row number, 1 to n. Queens at distinct positions (x1, y1) and (x2, y2) lie on the same diagonal if (x1- x2) and (y1- y2) have the same magnitude. They lie on the same row or column if x1= x2 or y1= y2, respectively. In each of these cases the queens have a collision if there is no other queen directly between them on the same diagonal, row, or column, respectively. For example, in Figure 2, the collisions are between the queens at (5, 1) and (4, 2), (4, 2) and (3, 3), (3, 3) and (2, 4), and finally (2, 4) and (1, 5). In Figure 3, the collisions are between the queens at (1, 8) and (4, 8), (4, 8) and (4, 7), (4, 7) and (6, 5), (7, 6) and (6, 5), and finally (6, 5) and (2, 1). Your task is to count queen collisions.

In many situations there are a number of queens in a regular pattern. For instance in Figure 1 there are 4 queens in a line at (1,1), (2, 3), (3, 5), and (4, 7). Each of these queens after the first at (1, 1) is one to the right and 2 up from the previous one. Three queens starting at (5, 2) follow a similar pattern. Noting these patterns can allow the positions of a large number of queens to be stated succinctly.

The input will consist of one to twenty data sets, followed by a line containing only 0.
The first line of a dataset contains blank separated positive integers n g, where n indicates an n x n board size, and g is the number of linear patterns of queens to be described, where n < 30000, and g < 250. The next g lines each contain five blank separated integers, k x y s t, representing a linear pattern of k queens at locations (x + i*s, y +i*t), for i = 0, 1, ..., k-1. The value of k is positive. If k is 1, then the values of s and t are irrelevant, and they will be given as 0. All queen positions will be on the board. The total number of queen positions among all the linear patterns will be no more than n, and all these queen positions will be distinct.

There is one line of output for each data set, containing only the number of collisions between the queens.
The sample input data set corresponds to the configuration in the Figures.

Take some care with your algorithm, or else your solution may take too long.